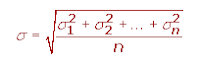Propiedades de la Esperanza Matemática:
La esperanza matemática consta de las siguientes propiedades principales:
1) El valor que se espera de la constante es igual a la misma:
E(C) = c Siendo C una constante, entonces tenemos que:
Ejemplo:
Ejemplo:
C = {4}
E(C) = 4
2) Sí X e Y son variables aleatorias, encontramos que:
E (X + Y) = E(X) + E(Y) Lo que indica la propiedad es que: el valor que se espera de la suma de las dos variables aleatorias, sea igual a la sumatoria de sus valores esperados.
Ejemplo:
X
|
1
|
2
|
3
|
4
|
F(X=x)
|
1/8
|
3/8
|
3/8
|
1/8
|
Y
|
1
|
2
|
F(X=x)
|
1/2
|
1/2
|
E(X) = 5 , E(Y)=7
E(X+Y)= 5+7 = 12
3) Si “ C ” es una constante y “ X ” una variable, encontramos que:
E(C . x) = C . E(x) Lo que india la propiedad es que: El valor que se espera del resultado de una constante por una variable aleatoria ( E(C.x) ) es igual al resultado de la constante por el valor que se espera de la variable ( C . E(x) ) .
Ejemplo:
C= {4} , E(x) = 6 Siendo C una Constante y X una variable aleatoria, entonces tenemos que:
E(C . x) = C . E(x)
E(4 . 6) = 4 . 6
24 = 24
4) Sí A y B son variables aleatorias independientes, encontramos que:
E( A . B ) = E(A) . E(B)
Ejemplo:
E(A) = 5 , E(B) = 7 Siendo A y B variables aleatorias independientes, entonces tenemos que:
E( A . B ) = E(A) . E(B)
E( A . B ) = 5 . 7
E( A . B ) = 35
Propiedades de la varianza:
La Varianza tiene las siguientes propiedades:
1) Var (C) = 0. Lo que indica la propiedad es que: La varianza de una constante es CERO. La varianza mide la dispersión, claro está que una constante no puede tener dispersión, por lo tanto la varianza es cero.
Ejemplo:
C= 5 Siendo C una constante, entonces tenemos que:
Var (C) = 0
2) Var(C.X) = C2 . Var(X) Lo que indica la propiedad es que: La varianza del producto de una constante multiplicada por una variable, será igual a la constante elevada al cuadrado multiplicada por la varianza de la variable.
Ejemplo:
C= 7 , X= 5 Siendo C una constante y X una variable aleatoria, entonces tenemos que:
Var(C.X) = C2 . Var(X)
Var(7 . 5) = 72 . Var(5)
Var(35) = 49 . 5
245 = 245
3) Sí X y Z son variables aleatorias cualquiera:
Var ( X + Z ) = Var (X) + Var (Z) + 2 Cov ( X, Y )
Teniendo en cuenta que la covarianza (Cov) de dos variables independientes es igual a CERO. Sí X y Z son dos variables independientes Cov ( X, Y ) = 0 por lo tanto:
Var ( X + Z ) = Var (X) + Var (Z)
La varianza de la suma de dos variables independientes es igual a la suma de varianzas.
Ejemplo:
Var(X)= 6
Var(Z)= 10
Var ( X + Z ) = Var (X) + Var (Z)
Var ( X + Z ) = 6 + 10
Var ( X + Z ) = 16
Desviación Típica
1) La desviación típica será siempre un valor positivo o cero, en el caso de que las puntuaciones sean iguales.
Ejemplo:
X=
|
6 + 6 + 6 + 6
|
= 6
| |||
4
| |||||
Ơ2=
|
(6-6)2 + (6-6)2 + (6-6)2 + (6-6)2
|
= 0
| |||
4
| |||||
Ơ=
|
√0
| ||||
Ơ=
|
0
| ||||
2)Si a todos los valores de la variable se les suma un número la desviación típica no varía.
Ejemplo:
X=
|
(8+4)
|
= 6
| ||
2
| ||||
Ơ2=
|
(8-6)2 + (4-6)2
|
= 4
| ||
2
| ||||
Ơ=
|
√4
| |||
Ơ=
|
2
| |||
Le sumamos +2 a todas las variables
X=
|
(10+6)
|
= 8
| ||
2
| ||||
Ơ2=
|
(10-8)2 + (6-8)2
|
= 4
| ||
2
| ||||
Ơ=
|
√4
| |||
Ơ=
|
2
| |||
3) Si todos los valores de la variable se multiplican por un número ladesviación típica queda multiplicada por dicho número.
Ejemplo:
X=
|
(4+8)
|
= 6
| ||
2
| ||||
Ơ2=
|
(4-6)2 + (8-6)2
|
= 4
| ||
2
| ||||
Ơ=
|
√4
| |||
Ơ=
|
2
| |||
Le multiplicamos x2 a todas las variables
X=
|
4(2)+8(2)
|
= 6(2)
| ||
2
| ||||
Ơ2=
| = 40 | |||
2
| ||||
Ơ=
|
√40
| |||
Ơ=
|
6 = 3.2
| |||
4) Si tenemos varias distribuciones con la misma media y conocemos sus respectivas desviaciones típicas se puede calcular la desviación típica total.